Dynamic Programming
[TOC]
参考网站 https://www.geeksforgeeks.org/
动态规划专题 https://www.geeksforgeeks.org/dynamic-programming/
1. DP Properties
- Overlapping Subproblems(重叠子问题)
- Optimal Substructure(最优子结构)
2. Steps to solve a DP
- Identify if it is a DP problem
- Decide a state expression with least parameters
- Formulate state relationship
- Do tabulation (Bottom Up) or add memoization (Top Down)
3. Basic Problems
3.1 Fibonacci numbers
The Fibonacci numbers are the numbers in the following integer sequence.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ……..
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
Fn = Fn-1 + Fn-2
with seed values
F0 = 0 and F1 = 1.
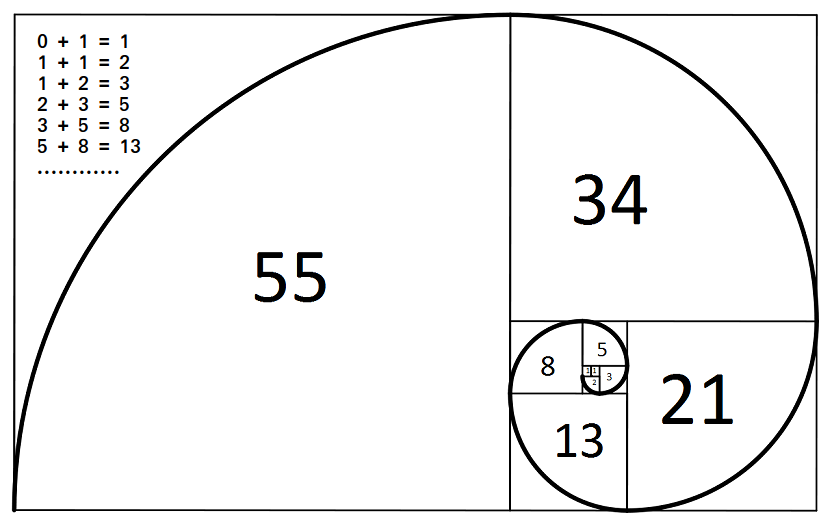
Given a number n, print n-th Fibonacci Number.
Input : n = 2
Output : 1
Input : n = 9
Output : 34
/*package whatever //do not write package name here */
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG {
private static final int MOD = 1000000007;
public static void main (String[] args) {
//code
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
int max = 0;
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
if (a[i] > max) max = a[i];
}
int[] dp = new int[max + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= max; i++) {
dp[i] = (dp[i - 2] + dp[i - 1]) % MOD;
}
for (int i = 0; i < n; i++) {
System.out.println(dp[a[i]]);
}
sc.close();
}
}
3.2 Binomial Coefficient
Following are common definition of Binomial Coefficients. 1) A binomial coefficient C(n, k) can be defined as the coefficient of X^k in the expansion of (1 + X)^n.
2) A binomial coefficient C(n, k) also gives the number of ways, disregarding order, that k objects can be chosen from among n objects; more formally, the number of k-element subsets (or k-combinations) of an n-element set.
The Problem Write a function that takes two parameters n and k and returns the value of Binomial Coefficient C(n, k). For example, your function should return 6 for n = 4 and k = 2, and it should return 10 for n = 5 and k = 2.
/*package whatever //do not write package name here */
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG {
private static final int MOD = 1000000007;
public static void main (String[] args) {
//code
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int n = sc.nextInt();
int r = sc.nextInt();
if (r > n) {
System.out.println(0);
} else {
System.out.println(solution(n, r));
}
}
sc.close();
}
private static int solution (int n, int r) {
r = Math.min(r, n - r);
int[][] dp = new int[n + 1][r + 1];
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= Math.min(i, r); j++) {
if (j == 0 || j == i) {
dp[i][j] = 1;
} else {
dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % MOD;
}
}
}
return dp[n][r];
}
}
Better Solution (Space: O(r))
import java.util.*;
class GFG {
private static final int MOD = 1000000007;
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int n = sc.nextInt();
int r = sc.nextInt();
if (r > n) {
System.out.println(0);
} else {
System.out.println(solution(n, r));
}
}
sc.close();
}
private static int solution (int n, int r) {
r = Math.min(r, n - r);
int[] dp = new int[r + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = Math.min(i, r); j > 0; j--) {
dp[j] += dp[j - 1];
dp[j] %= MOD;
}
}
return dp[r];
}
}
3.3 Longest Common Subsequence
LCS Problem Statement: Given two sequences, find the length of longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous. For example, “abc”, “abg”, “bdf”, “aeg”, ‘”acefg”, .. etc are subsequences of “abcdefg”. So a string of length n has 2^n different possible subsequences.
It is a classic computer science problem, the basis of diff (a file comparison program that outputs the differences between two files), and has applications in bioinformatics.
Examples: LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3. LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int len1 = sc.nextInt();
int len2 = sc.nextInt();
sc.nextLine();
String str1 = sc.nextLine();
String str2 = sc.nextLine();
System.out.println(solution(len1, len2, str1, str2));
}
sc.close();
}
private static int solution(int len1, int len2, String str1, String str2) {
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
Printing Longest Common Subsequence
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int len1 = sc.nextInt();
int len2 = sc.nextInt();
sc.nextLine();
String str1 = sc.nextLine();
String str2 = sc.nextLine();
System.out.println(solution(len1, len2, str1, str2));
}
sc.close();
}
private static int solution(int len1, int len2, String str1, String str2) {
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// Print LCS
StringBuffer sb = new StringBuffer();
int i = len1;
int j = len2;
while (i > 0 && j > 0) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
sb.append(str1.charAt(i - 1));
i--;
j--;
} else if (dp[i][j] == dp[i - 1][j]) {
i--;
} else {
j--;
}
}
System.out.println(sb.reverse().toString());
return dp[len1][len2];
}
}
3.4 Longest Repeated Subsequence
Given a string, print the longest repeating subsequence such that the two subsequence don’t have same string character at same position, i.e., any i’th character in the two subsequences shouldn’t have the same index in the original string.

More Examples:
Input: str = "aabb"
Output: "ab"
Input: str = "aab"
Output: "a"
The two subsequence are 'a'(first) and 'a'
(second). Note that 'b' cannot be considered
as part of subsequence as it would be at same
index in both.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int len = sc.nextInt();
sc.nextLine();
String str = sc.nextLine();
System.out.println(solution(len, str));
}
sc.close();
}
private static int solution(int len, String str) {
int[][] dp = new int[len + 1][len + 1];
for (int i = 1; i <= len; i++) {
for (int j = 1; j <= len; j++) {
if (str.charAt(i - 1) == str.charAt(j - 1) && i != j) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len][len];
}
}
How to print the subsequence?
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int len = sc.nextInt();
sc.nextLine();
String str = sc.nextLine();
System.out.println(solution(len, str));
}
sc.close();
}
private static int solution(int len, String str) {
int[][] dp = new int[len + 1][len + 1];
for (int i = 1; i <= len; i++) {
for (int j = 1; j <= len; j++) {
if (str.charAt(i - 1) == str.charAt(j - 1) && i != j) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// Print LRS
StringBuilder sb = new StringBuilder();
int i = len;
int j = len;
while (i > 0 && j > 0) {
if (dp[i][j] == dp[i - 1][j - 1] + 1) {
sb.append(str.charAt(i - 1));
i--;
j--;
} else if (dp[i][j] == dp[i - 1][j]) {
i--;
} else {
j--;
}
}
System.out.println(sb.reverse().toString());
return dp[len][len];
}
}
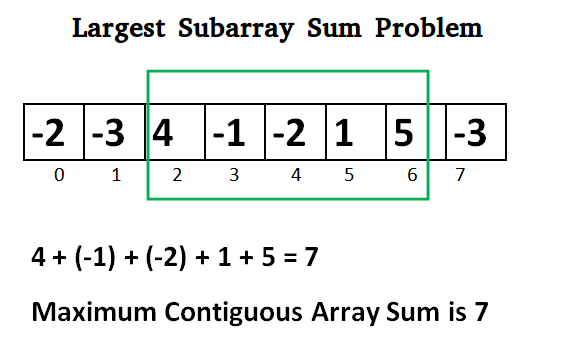
3.5 Largest Sum Contiguous Subarray
Write an efficient C program to find the sum of contiguous subarray within a one-dimensional array of numbers which has the largest sum.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int n = sc.nextInt();
sc.nextLine();
String str = sc.nextLine();
System.out.println(solution(n, str));
}
sc.close();
}
private static int solution(int n, String str) {
String[] a = str.split(" ");
int max = Integer.parseInt(a[0]);
int currMax = max;
for (int i = 1; i < n; i++) {
int t = Integer.parseInt(a[i]);
currMax = Math.max(currMax + t, t);
max = Math.max(max, currMax);
}
return max;
}
}
3.6 Ugly numbers
Ugly numbers are numbers whose only prime factors are 2, 3 or 5. The sequence 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, … shows the first 11 ugly numbers. By convention, 1 is included.
Given a number n, the task is to find n’th Ugly number.
Input : n = 7
Output : 8
Input : n = 10
Output : 12
Input : n = 15
Output : 24
Input : n = 150
Output : 5832
Practice: https://practice.geeksforgeeks.org/problems/ugly-numbers/0
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int i = 0; i < T; i++) {
int n = sc.nextInt();
System.out.println(solution(n));
}
sc.close();
}
private static int solution(int n) {
int[] a = new int[n];
a[0] = 1;
int i2 = 0, i3 = 0, i5 = 0;
int n2 = a[i2] * 2;
int n3 = a[i3] * 3;
int n5 = a[i5] * 5;
for (int i = 1; i < n; i++) {
a[i] = Math.min(n2, Math.min(n3, n5));
if (a[i] == n2) {
i2++;
n2 = a[i2] * 2;
}
if (a[i] == n3) {
i3++;
n3 = a[i3] * 3;
}
if (a[i] == n5) {
i5++;
n5 = a[i5] * 5;
}
}
return a[n - 1];
}
}
3.7 Maximum size square sub-matrix with all 1s
Given a binary matrix, find out the maximum size square sub-matrix with all 1s.
For example, consider the below binary matrix.

import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int m = sc.nextInt();
int[][] a = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = sc.nextInt();
}
}
System.out.println(solution(n, m, a));
}
sc.close();
}
private static int solution(int n, int m, int[][] a) {
int[][] dp = new int[n + 1][m + 1];
int max = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i - 1][j - 1] == 1) {
dp[i][j] = Math.min(dp[i - 1][j - 1],
Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
max = Math.max(max, dp[i][j]);
}
}
}
return max;
}
}
3.8 Longest Increasing Subsequence
Let us discuss Longest Increasing Subsequence (LIS) problem as an example problem that can be solved using Dynamic Programming.
The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order. For example, the length of LIS for {10, 22, 9, 33, 21, 50, 41, 60, 80} is 6 and LIS is {10, 22, 33, 50, 60, 80}.

More Examples:
Input : arr[] = {3, 10, 2, 1, 20}
Output : Length of LIS = 3
The longest increasing subsequence is 3, 10, 20
Input : arr[] = {3, 2}
Output : Length of LIS = 1
The longest increasing subsequences are {3} and {2}
Input : arr[] = {50, 3, 10, 7, 40, 80}
Output : Length of LIS = 4
The longest increasing subsequence is {3, 7, 40, 80}
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
System.out.println(solution(n, a));
}
sc.close();
}
private static int solution(int n, int[] a) {
int[] lis = new int[n];
for (int i = 0; i < n; i++) {
lis[i] = 1;
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (a[j] < a[i] && lis[i] < lis[j] + 1) {
lis[i] = lis[j] + 1;
}
}
}
int max = 0;
for (int i = 0; i < n; i++) {
max = Math.max(max, lis[i]);
}
return max;
}
}
3.9 Min Cost Path
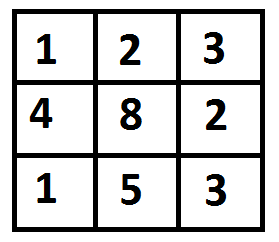
Given a cost matrix cost[][] and a position (m, n) in cost[][], write a function that returns cost of minimum cost path to reach (m, n) from (0, 0). Each cell of the matrix represents a cost to traverse through that cell. Total cost of a path to reach (m, n) is sum of all the costs on that path (including both source and destination). You can only traverse down, right and diagonally lower cells from a given cell, i.e., from a given cell (i, j), cells (i+1, j), (i, j+1) and (i+1, j+1) can be traversed. You may assume that all costs are positive integers.
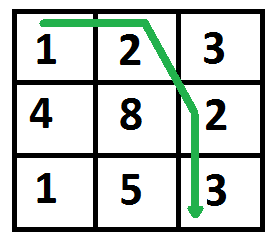
For example, in the following figure, what is the minimum cost path to (2, 2)?
The path with minimum cost is highlighted in the following figure. The path is (0, 0) –> (0, 1) –> (1, 2) –> (2, 2). The cost of the path is 8 (1 + 2 + 2 + 3).
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[][] a = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = sc.nextInt();
}
}
System.out.println(solution(n, a));
}
sc.close();
}
private static int solution(int n, int[][] a) {
int[][] dp = new int[n][n];
dp[0][0] = a[0][0];
for (int i = 1; i < n; i++) {
dp[0][i] = dp[0][i - 1] + a[0][i];
}
for (int i = 1; i < n; i++) {
dp[i][0] = dp[i - 1][0] + a[i][0];
}
for (int i = 1; i < n; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i - 1][j - 1],
Math.min(dp[i - 1][j], dp[i][j - 1])) + a[i][j];
}
}
return dp[n - 1][n - 1];
}
}
3.10 Coin change problem
Given a value N, if we want to make change for N cents, and we have infinite supply of each of S = { S1, S2, .. , Sm} valued coins, how many ways can we make the change? The order of coins doesn’t matter.
For example, for N = 4 and S = {1,2,3}, there are four solutions: {1,1,1,1},{1,1,2},{2,2},{1,3}. So output should be 4. For N = 10 and S = {2, 5, 3, 6}, there are five solutions: {2,2,2,2,2}, {2,2,3,3}, {2,2,6}, {2,3,5} and {5,5}. So the output should be 5.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
int target = sc.nextInt();
System.out.println(solution(n, a, target));
}
sc.close();
}
private static int solution(int n, int[] a, int target) {
Arrays.sort(a);
int[] dp = new int[target + 1];
dp[0] = 1;
for (int i = 0; i < n; i++) {
for (int j = a[i]; j <= target; j++) {
dp[j] = dp[j] + dp[j - a[i]];
}
}
return dp[target];
}
}
3.11 Minimum number of edits ( operations ) require to convert string 1 to string 2
Given two strings str1 and str2 and below operations that can performed on str1. Find minimum number of edits (operations) required to convert ‘str1’ into ‘str2’.
- Insert
- Remove
- Replace
All of the above operations are of equal cost. Examples:
Input: str1 = "geek", str2 = "gesek"
Output: 1
We can convert str1 into str2 by inserting a 's'.
Input: str1 = "cat", str2 = "cut"
Output: 1
We can convert str1 into str2 by replacing 'a' with 'u'.
Input: str1 = "sunday", str2 = "saturday"
Output: 3
Last three and first characters are same. We basically
need to convert "un" to "atur". This can be done using
below three operations.
Replace 'n' with 'r', insert t, insert a
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int len1 = sc.nextInt();
int len2 = sc.nextInt();
sc.nextLine();
String str1 = sc.nextLine();
String str2 = sc.nextLine();
System.out.println(solution(len1, len2, str1, str2));
}
sc.close();
}
private static int solution(int len1, int len2, String str1, String str2) {
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
dp[i][0] = i;
}
for (int j = 1; j <= len2; j++) {
dp[0][j] = j;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j - 1],
Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
}
}
return dp[len1][len2];
}
}
3.12 Cutting a Rod
Given a rod of length n inches and an array of prices that contains prices of all pieces of size smaller than n.Determine the maximum value obtainable by cutting up the rod and selling the pieces. For example, if length of the rod is 8 and the values of different pieces are given as following, then the maximum obtainable value is 22 (by cutting in two pieces of lengths 2 and 6)
length | 1 2 3 4 5 6 7 8
--------------------------------------------
price | 1 5 8 9 10 17 17 20
And if the prices are as following, then the maximum obtainable value is 24 (by cutting in eight pieces of length 1)
length | 1 2 3 4 5 6 7 8
--------------------------------------------
price | 3 5 8 9 10 17 17 20
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
System.out.println(solution(n, a));
}
sc.close();
}
private static int solution(int n, int[] a) {
int[] dp = new int[n + 1];
for (int i = 0; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
dp[j] = Math.max(dp[j], dp[j - i - 1] + a[i]);
}
}
return dp[n];
}
}
3.13 Subset Sum Problem
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Examples: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True //There is a subset (4, 5) with sum 9.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
int sum = sc.nextInt();
System.out.println(solution(n, a, sum));
}
sc.close();
}
private static boolean solution(int n, int[] a, int sum) {
boolean[][] dp = new boolean[sum + 1][n + 1];
for (int i = 0; i <= n; i++) {
dp[0][i] = true;
}
for (int i = 1; i <= sum; i++) {
dp[i][0] = false;
}
for (int i = 1; i <= sum; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i][j - 1];
if (a[j - 1] <= i) {
dp[i][j] = dp[i][j] || dp[i - a[j - 1]][j - 1];
}
}
}
return dp[sum][n];
}
}
3.14 Minimum number of jumps to reach end
Given an array of integers where each element represents the max number of steps that can be made forward from that element. Write a function to return the minimum number of jumps to reach the end of the array (starting from the first element). If an element is 0, then cannot move through that element.
Example:
Input: arr[] = {1, 3, 5, 8, 9, 2, 6, 7, 6, 8, 9}
Output: 3 (1-> 3 -> 8 ->9)
First element is 1, so can only go to 3. Second element is 3, so can make at most 3 steps eg to 5 or 8 or 9.
import java.util.*;
class GFG {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
System.out.println(solution(n, a));
}
sc.close();
}
private static int solution(int n, int[] a) {
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
dp[i] = Integer.MAX_VALUE;
}
for (int i = 0; i < n; i++) {
for (int j = 1; j <= a[i] && i + j < n; j++) {
if (dp[i] != Integer.MAX_VALUE) {
dp[i + j] = Math.min(dp[i + j], dp[i] + 1);
}
}
}
return dp[n - 1] == Integer.MAX_VALUE ? -1 : dp[n - 1];
}
}
3.15 Assembly line scheduling
3.16 Maximum Sum Increasing Subsequence
Given an array of n positive integers. Write a program to find the sum of maximum sum subsequence of the given array such that the intgers in the subsequence are sorted in increasing order. For example, if input is {1, 101, 2, 3, 100, 4, 5}, then output should be 106 (1 + 2 + 3 + 100), if the input array is {3, 4, 5, 10}, then output should be 22 (3 + 4 + 5 + 10) and if the input array is {10, 5, 4, 3}, then output should be 10
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
System.out.println(solution(n, a));
}
sc.close();
}
private static int solution(int n, int[] a) {
int[] dp = new int[n];
int max = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
dp[i] = a[i];
for (int j = 0; j < i; j++) {
if (a[j] < a[i]) {
dp[i] = Math.max(dp[i], dp[j] + a[i]);
}
}
max = Math.max(max, dp[i]);
}
return max;
}
}
3.17 Maximum Length Chain of Pairs
| You are given n pairs of numbers. In every pair, the first number is always smaller than the second number. A pair (c, d) can follow another pair (a, b) if b < c. Chain of pairs can be formed in this fashion. Find the longest chain which can be formed from a given set of pairs. Source: [Amazon Interview | Set 2](https://www.geeksforgeeks.org/archives/23038) |
For example, if the given pairs are {5, 24}, {39, 60}, {15, 28}, {27, 40}, {50, 90} , then the longest chain that can be formed is of length 3, and the chain is {5, 24}, {27, 40}, {50, 90}
class Pair{
int a;
int b;
public Pair(int a, int b) {
this.a = a;
this.b = b;
}
// This function assumes that arr[] is sorted in increasing order
// according the first (or smaller) values in pairs.
static int maxChainLength(Pair arr[], int n)
{
int i, j, max = 0;
int mcl[] = new int[n];
/* Initialize MCL (max chain length) values for all indexes */
for ( i = 0; i < n; i++ )
mcl[i] = 1;
/* Compute optimized chain length values in bottom up manner */
for ( i = 1; i < n; i++ )
for ( j = 0; j < i; j++ )
if ( arr[i].a > arr[j].b && mcl[i] < mcl[j] + 1)
mcl[i] = mcl[j] + 1;
// mcl[i] now stores the maximum chain length ending with pair i
/* Pick maximum of all MCL values */
for ( i = 0; i < n; i++ )
if ( max < mcl[i] )
max = mcl[i];
return max;
}
/* Driver program to test above function */
public static void main(String[] args)
{
Pair arr[] = new Pair[] {new Pair(5,24), new Pair(15, 25),
new Pair (27, 40), new Pair(50, 60)};
System.out.println("Length of maximum size chain is " +
maxChainLength(arr, arr.length));
}
}
3.18 Longest Common Substring
Given two strings ‘X’ and ‘Y’, find the length of the longest common substring.
Examples :
Input : X = "GeeksforGeeks", y = "GeeksQuiz"
Output : 5
The longest common substring is "Geeks" and is of
length 5.
Input : X = "abcdxyz", y = "xyzabcd"
Output : 4
The longest common substring is "abcd" and is of
length 4.
Input : X = "zxabcdezy", y = "yzabcdezx"
Output : 6
The longest common substring is "abcdez" and is of
length 6.

import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int len1 = sc.nextInt();
int len2 = sc.nextInt();
sc.nextLine();
String str1 = sc.nextLine();
String str2 = sc.nextLine();
System.out.println(solution(len1, len2, str1, str2));
}
sc.close();
}
private static int solution(int len1, int len2, String str1, String str2) {
int[][] dp = new int[len1 + 1][len2 + 1];
int max = 0;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
max = Math.max(max, dp[i][j]);
}
}
}
return max;
}
}
3.19 Count all possible paths from top left to bottom right of a mXn matrix
The problem is to count all the possible paths from top left to bottom right of a mXn matrix with the constraints that *from each cell you can either move only to right or down*
import java.util.*;
class GFG {
private static final int MOD = 1000000007;
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
int m = sc.nextInt();
System.out.println(solution(n, m));
}
sc.close();
}
private static int solution(int n, int m) {
int[][] dp = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % MOD;
}
}
}
return dp[n - 1][m - 1];
}
}
3.20 nth Catalan Number
Reference: 卡特兰数(Catalan)及其应用
Catalan numbers are a sequence of natural numbers that occurs in many interesting counting problems like following.
1) Count the number of expressions containing n pairs of parentheses which are correctly matched. For n = 3, possible expressions are ((())), ()(()), ()()(), (())(), (()()).
2) Count the number of possible Binary Search Trees with n keys (See this)
3) Count the number of full binary trees (A rooted binary tree is full if every vertex has either two children or no children) with n+1 leaves.
See this for more applications.
The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
System.out.println(solution(n));
}
sc.close();
}
private static int solution(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < i; j++) {
dp[i] += dp[j] * dp[i - j];
}
}
return dp[n];
}
}
3.21 Count number of ways to reach a given score in a game
This problem is a variation of coin change problem.
3.22 Tiling Problem
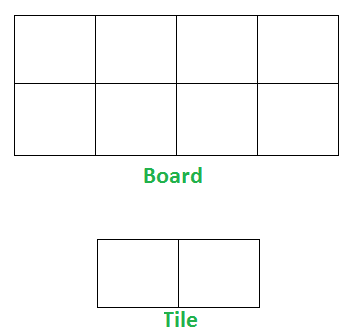
Given a “2 x n” board and tiles of size “2 x 1”, count the number of ways to tile the given board using the 2 x 1 tiles. A tile can either be placed horizontally i.e., as a 1 x 2 tile or vertically i.e., as 2 x 1 tile.
Examples:
Input n = 3
Output: 3
Explanation:
We need 3 tiles to tile the board of size 2 x 3.
We can tile the board using following ways
1) Place all 3 tiles vertically.
2) Place first tile vertically and remaining 2 tiles horizontally.
3) Place first 2 tiles horizontally and remaining tiles vertically
Input n = 4
Output: 5
Explanation:
For a 2 x 4 board, there are 5 ways
1) All 4 vertical
2) All 4 horizontal
3) First 2 vertical, remaining 2 horizontal
4) First 2 horizontal, remaining 2 vertical
5) Corner 2 vertical, middle 2 horizontal
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int n = sc.nextInt();
System.out.println(solution(n));
}
sc.close();
}
private static long solution(int n) {
if (n <= 2) return n;
long[] dp = new long[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 2] + dp[i - 1];
}
return dp[n];
}
}
3.23 Count even length binary sequences with same sum of first and second half bits
Given a number n, find count of all binary sequences of length 2n such that sum of first n bits is same as sum of last n bits.
Examples:
Input: n = 1
Output: 2
There are 2 sequences of length 2*n, the
sequences are 00 and 11
Input: n = 2
Output: 2
There are 6 sequences of length 2*n, the
sequences are 0101, 0110, 1010, 1001, 0000
and 1111
// A memoization based C++ program to
// count even length binary sequences
// such that the sum of first and
// second half bits is same
import java.io.*;
class GFG {
// A lookup table to store the results of
// subproblems
static int lookup[][] = new int[1000][1000];
// dif is diference between sums of first
// n bits and last n bits i.e.,
// dif = (Sum of first n bits) - (Sum of last n bits)
static int countSeqUtil(int n, int dif)
{
// We can't cover diference of
// more than n with 2n bits
if (Math.abs(dif) > n)
return 0;
// n == 1, i.e., 2 bit long sequences
if (n == 1 && dif == 0)
return 2;
if (n == 1 && Math.abs(dif) == 1)
return 1;
// Check if this subbproblem is already
// solved n is added to dif to make
// sure index becomes positive
if (lookup[n][n+dif] != -1)
return lookup[n][n+dif];
int res = // First bit is 0 & last bit is 1
countSeqUtil(n-1, dif+1) +
// First and last bits are same
2*countSeqUtil(n-1, dif) +
// First bit is 1 & last bit is 0
countSeqUtil(n-1, dif-1);
// Store result in lookup table
// and return the result
return lookup[n][n+dif] = res;
}
// A Wrapper over countSeqUtil(). It mainly
// initializes lookup table, then calls
// countSeqUtil()
static int countSeq(int n)
{
// Initialize all entries of lookup
// table as not filled
// memset(lookup, -1, sizeof(lookup));
for(int k = 0; k < lookup.length; k++)
{
for(int j = 0; j < lookup.length; j++)
{
lookup[k][j] = -1;
}
}
// call countSeqUtil()
return countSeqUtil(n, 0);
}
// Driver program
public static void main(String[] args)
{
int n = 2;
System.out.println("Count of sequences is "
+ countSeq(2));
}
}
// This code is contributed by Prerna Saini
3.24 Find number of solutions of a linear equation of n variables
This problem is a variation of coin change problem.
3.25 Bell Numbers (Number of ways to Partition a Set)
3.26 Compute nCr % p
C(n, r)%p = [ C(n-1, r-1)%p + C(n-1, r)%p ] % p
C(n, 0) = C(n, n) = 1
3.27 Permutation Coefficient
Permutation refers to the process of arranging all the members of a given set to form a sequence. The number of permutations on a set of n elements is given by n! , where “!” represents factorial. The Permutation Coefficient represented by P(n, k) is used to represent the number of ways to obtain an ordered subset having k elements from a set of n elements.
Mathematically it’s given as:
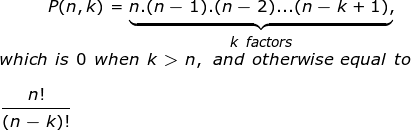
Image Source : Wiki
Examples:
P(10, 2) = 90
P(10, 3) = 720
P(10, 0) = 1
P(10, 1) = 10
The coefficient can also be computed recursively using the below recursive formula:
P(n, k) = P(n-1, k) + k* P(n-1, k-1)
3.28 Count number of ways to fill a “n x 4” grid using “1 x 4” tiles
Given a number n, count number of ways to fill a n x 4 grid using 1 x 4 tiles.
Examples:
Input : n = 1
Output : 1
Input : n = 2
Output : 1
We can only place both tiles horizontally
Input : n = 3
Output : 1
We can only place all tiles horizontally.
Input : n = 4
Output : 2
The two ways are :
1) Place all tiles horizontally
2) Place all tiles vertically.
Input : n = 5
Output : 3
We can fill a 5 x 4 grid in following ways :
1) Place all 5 tiles horizontally
2) Place first 4 vertically and 1 horizontally.
3) Place first 1 horizontally and 4 horizontally.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int N = sc.nextInt();
System.out.println(N);
}
sc.close();
}
private static int solution(int N) {
if (N <= 3) return 1;
if (N == 4) return 2;
int[] dp = new int[N + 1];
dp[1] = 1;
dp[2] = 1;
dp[3] = 1;
dp[4] = 2;
for (int i = 5; i <= N; i++) {
dp[i] = dp[i - 1] + dp[i - 4];
}
return dp[N];
}
}
3.29 A Space Optimized Solution of LCS
One important observation in above simple implementation is, in each iteration of outer loop we only, need values from all columns of previous row. So there is no need of storing all rows in our DP matrix, we can just store two rows at a time and use them, in that way used space will reduce from L[m+1][n+1] to L[2][n+1]. Below is C++ implementation of this idea.
3.30 Find maximum length Snake sequence
3.31 Minimum cost to fill given weight in a bag
You are given a bag of size W kg and you are provided costs of packets different weights of oranges in array cost[] where cost[i] is basically cost of ‘i’ kg packet of oranges. Where cost[i] = -1 means that ‘i’ kg packet of orange is unavailable
Find the minimum total cost to buy exactly W kg oranges and if it is not possible to buy exactly W kg oranges then print -1. It may be assumed that there is infinite supply of all available packet types.
Note : array starts from index 1. Examples:
Input : W = 5, cost[] = {20, 10, 4, 50, 100}
Output : 14
We can choose two oranges to minimize cost. First
orange of 2Kg and cost 10. Second orange of 3Kg
and cost 4.
Input : W = 5, cost[] = {1, 10, 4, 50, 100}
Output : 5
We can choose five oranges of weight 1 kg.
Input : W = 5, cost[] = {1, 2, 3, 4, 5}
Output : 5
Costs of 1, 2, 3, 4 and 5 kg packets are 1, 2, 3,
4 and 5 Rs respectively.
We choose packet of 5kg having cost 5 for minimum
cost to get 5Kg oranges.
Input : W = 5, cost[] = {-1, -1, 4, 5, -1}
Output : -1
Packets of size 1, 2 and 5 kg are unavailable
because they have cost -1. Cost of 3 kg packet
is 4 Rs and of 4 kg is 5 Rs. Here we have only
weights 3 and 4 so by using these two we can
not make exactly W kg weight, therefore answer
is -1.
import java.util.*;
class GFG {
public static void main (String[] args) {
Scanner sc = new Scanner(System.in);
int T = sc.nextInt();
for (int t = 0; t < T; t++) {
int N = sc.nextInt();
int W = sc.nextInt();
int[] a = new int[N];
for (int i = 0; i < N; i++) {
a[i] = sc.nextInt();
}
System.out.println(solution(N, W, a));
}
sc.close();
}
private static int solution(int N, int W, int[] a) {
int[][] dp = new int[N + 1][W + 1];
for (int i = 0; i <= N; i++) {
dp[i][0] = Integer.MAX_VALUE;
}
for (int j = 1; j <= W; j++) {
dp[0][j] = Integer.MAX_VALUE;
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= W; j++) {
if (a[i - 1] == -1 || j < i || dp[i][j - 1] == Integer.MAX_VALUE) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.min(dp[i][j - i] + a[i - 1], dp[i - 1][j]);
}
}
}
return dp[N][W] == Integer.MAX_VALUE ? -1 : dp[N][W];
}
}